Решение квадратных уравнений с помощью циркуля и линейки
Предлагаем следующий способ нахождения корней квадратного уравнения \(ах^2 + bх + с = 0 \) с помощью циркуля и линейки.
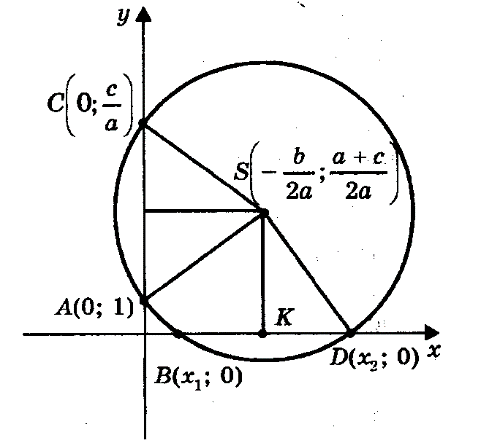 Допустим, что искомая окружность пересекает ось абсцисс в точках \(В(х_1; 0 ) \) и \(D (х_2; 0) \), где \(х_1 \) и \(х_2 \) – корни уравнения \( ах^2 + bх + с = 0 \), и проходит через точки \(A(0; 1) \) и \(C(0; \frac{c}{a}) \) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда \(OC = \frac{ОB * OD}{OA} = \frac{x_1 * x_2}{1} = \frac{c}{a} \) Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому \(SK = \frac{x_1 + x_2}{2} = \frac{-\frac{b}{a}}{2} = -\frac{b}{2a}; \) \(SF = \frac{y_1 + y_2}{2} = \frac{1 + \frac{c}{a}}{2} = \frac{a + c}{2a}; \)
Допустим, что искомая окружность пересекает ось абсцисс в точках \(В(х_1; 0 ) \) и \(D (х_2; 0) \), где \(х_1 \) и \(х_2 \) – корни уравнения \( ах^2 + bх + с = 0 \), и проходит через точки \(A(0; 1) \) и \(C(0; \frac{c}{a}) \) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда \(OC = \frac{ОB * OD}{OA} = \frac{x_1 * x_2}{1} = \frac{c}{a} \) Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому \(SK = \frac{x_1 + x_2}{2} = \frac{-\frac{b}{a}}{2} = -\frac{b}{2a}; \) \(SF = \frac{y_1 + y_2}{2} = \frac{1 + \frac{c}{a}}{2} = \frac{a + c}{2a}; \)
Итак:
1) построим точки \(s(-\frac{b}{2a};\frac{a + c}{2a}) \) (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS>SK, или R>a + c/2a), окружность пересекает ось Ох в двух точках \( ( рис. а ) \) \( В(х_1; 0) и D(х_2; 0) \) , где \(х_1 \) и \(х_2 \) – корни квадратного уравнения \( ах^2 + bх + с = 0 \) .
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох \( ( рис. б ) \) в точке (В(х_1; 0)), где (х_1) - корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра AS<;SB;R<(a+C)/2a окружность не имеет общих точек с осью абсцисс \( ( рис. в ) \) , в этом случае уравнение не имеет решения.
окружность не имеет общих точек с осью абсцисс \( ( рис. в ) \) , в этом случае уравнение не имеет решения.
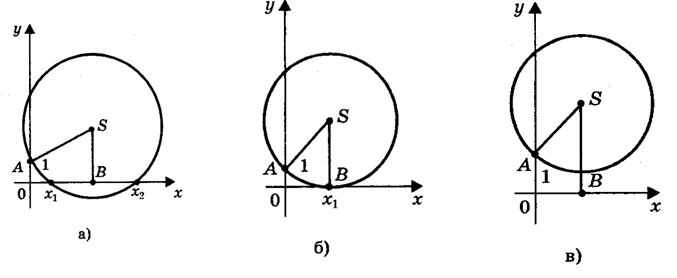
Два решения \( х_1 \) и \(х_2\).
Одно решение \( х_1. \)
Нет решения.
1)Решим уравнение \(х^2 – 2х – 3 = 0 \)
построим точки \(S (-\frac{b}{2a}; \frac{a+c}{2a}) \) — центр окружности и \( A(0;1) \) ;
\( x = -\frac{b}{2a} = -\frac{-2}{2} = 1 \\ y = \frac{a+c}{2a} = \frac{1-3}{2} = -1 \)
проведем окружность с центром \( S(1;–1) \) и радиусом SA, где \( A(0;1) \) ; \(x_1= -1; x_2=3 \)
Ответ: -1; 3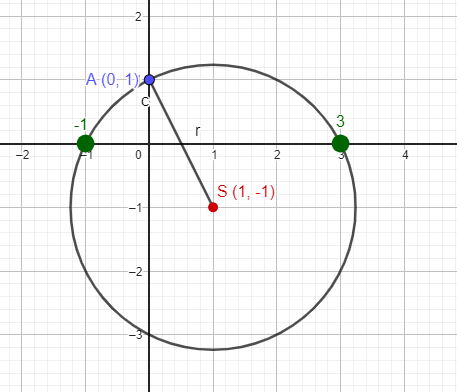
2)Решим уравнение \(х^2 – 5х + 4 = 0 \)
построим точки \(S (-\frac{b}{2a}; \frac{a+c}{2a}) \) — центр окружности и \( A(0;1) \) ;
\( x = -\frac{b}{2a} = -\frac{5}{2} = 2,5 \\ y = \frac{a+c}{2a} = \frac{1+4}{2} = 2,5 \)
проведем окружность с центром \( S(2,5;2,5) \) и радиусом SA, где \( A(0;1) \) ; \(x_1= 1; x_2=4 \)
Ответ: 1; 4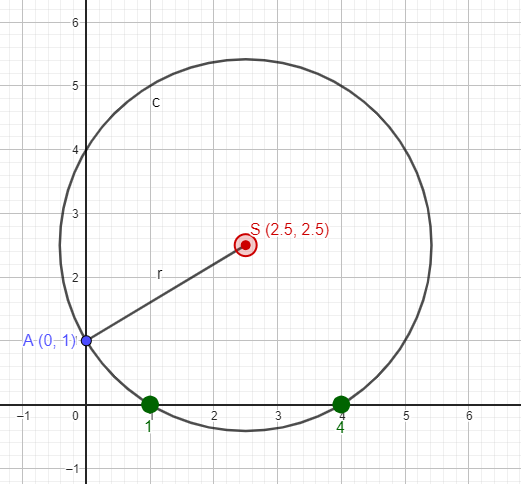
3)Решим уравнение \(х^2 + 4х + 4 = 0 \)
построим точки \(S (-\frac{b}{2a}; \frac{a+c}{2a}) \) — центр окружности и \( A(0;1) \) ;
\( x = -\frac{b}{2a} = \frac{-4}{2} = -2 \\ y = \frac{a+c}{2a} = \frac{1+4}{2} = 2,5 \)
проведем окружность с центром \( S(-2;2,5) \) и радиусом SA, где \( A(0;1) \) ; \(х= -2 \)
Ответ: -2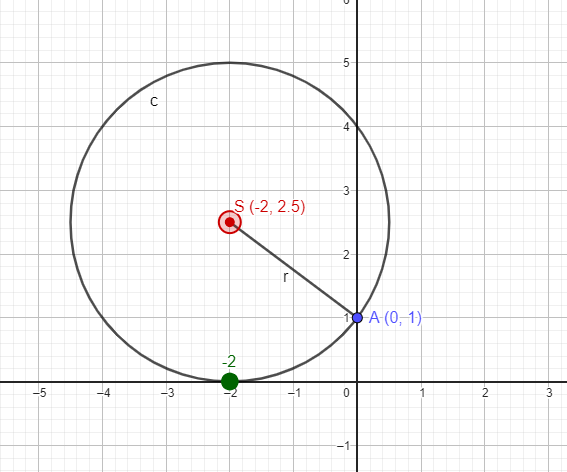
4)Решим уравнение \(х^2 – 2х – 3 = 0 \)
построим точки \(S (-\frac{b}{2a}; \frac{a+c}{2a}) \) — центр окружности и \( A(0;1) \) ;
\( x = -\frac{b}{2a} = \frac{2}{2} = 1 \\ y = \frac{a+c}{2a} = \frac{1+3}{2} = 2 \)
проведем окружность с центром \( S(1;2) \) и радиусом SA, где \( A(0;1) \) ;
Ответ: уравнение не имеет решения.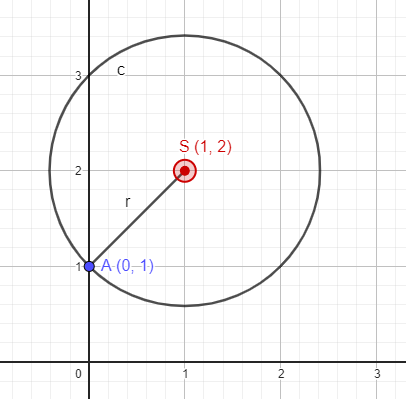
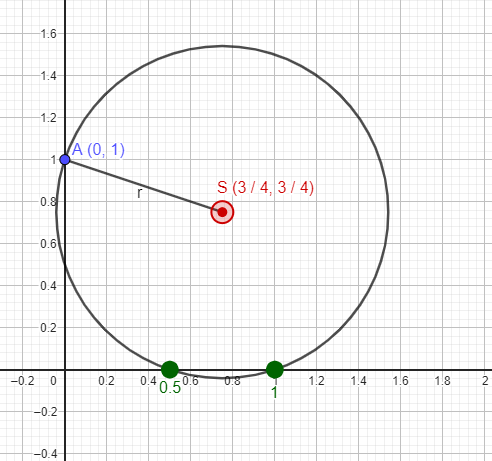
5)Решим уравнение \(х^2 – 2х – 3 = 0 \)
построим точки \(S (-\frac{b}{2a}; \frac{a+c}{2a}) \) — центр окружности и \( A(0;1) \) ;
\( x = -\frac{b}{2a} = \frac{3}{4} = 1 \\ y = \frac{a+c}{2a} = \frac{2+1}{4} = \frac{3}{4} \)
проведем окружность с центром \(S(\frac{3}{4};\frac{3}{4}) \) и радиусом SA, где \( A(0;1) \) ; \( x_1 = 0,5; x_2=1 \)
Ответ: 0,5; 1