Графический метод

Используя знания о квадратичной и линейной функциях и их графиках, можно решить квадратное уравнение так называемым функционально-графическим методом. Причем, некоторые квадратные уравнения можно решить различными способами, рассмотрим эти способы на примере одного квадратного уравнения.

1 способ. \(3x^2+4x-7=0,\)
\(x^2 + \frac{4}{3}x - \frac{7}{3} = 0 ⇔ x^2 = \frac{7}{3} - \frac{4}{3}x\)
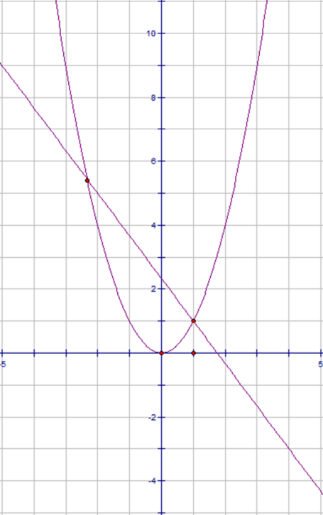
Построим графики функции\(y = x^2\) и \(y = \frac{7}{3} - \frac{4}{3}x\)в одной системе координат. Абсциссы точек пересечения этих двух графиков являются корнями данного уравнения.
\(x_1 = -2\frac{1}{3}, x_2 = 1\)

2 способ. \(3x^2+4x-7=0,\)
\(x^2 + \frac{4}{3}x - \frac{7}{3} = 0; ⇔ x^2 - \frac{7}{3} = -\frac{4}{3}x\)
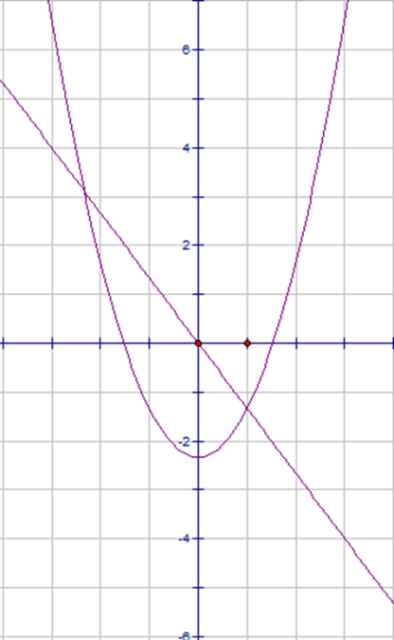
Построим графики функции\(y = x^2 - \frac{7}{3}\) и \(y = -\frac{4}{3}x \)в одной системе координат. Абсциссы точек пересечения этих двух графиков являются корнями данного уравнения.
\(x_1 = -2\frac{1}{3}, x_2 = 1\)

3 способ. \(3x^2+4x-7=0, | :х\)
\(3x + 4 - \frac{7}{x} = 0\)
Построим графики функции\(y = 3x + 4\) и \(y = \frac{7}{x}\)в одной системе координат. Абсциссы точек пересечения этих двух графиков являются корнями данного уравнения.
\(x_1 = -2\frac{1}{3}, x_2 = 1\)